Basic Architecture

Note

Here g(\vec{x}) is any activation function

Multiplicative Modules

These modules lets us combine outputs from other networks to modify a behaviour.

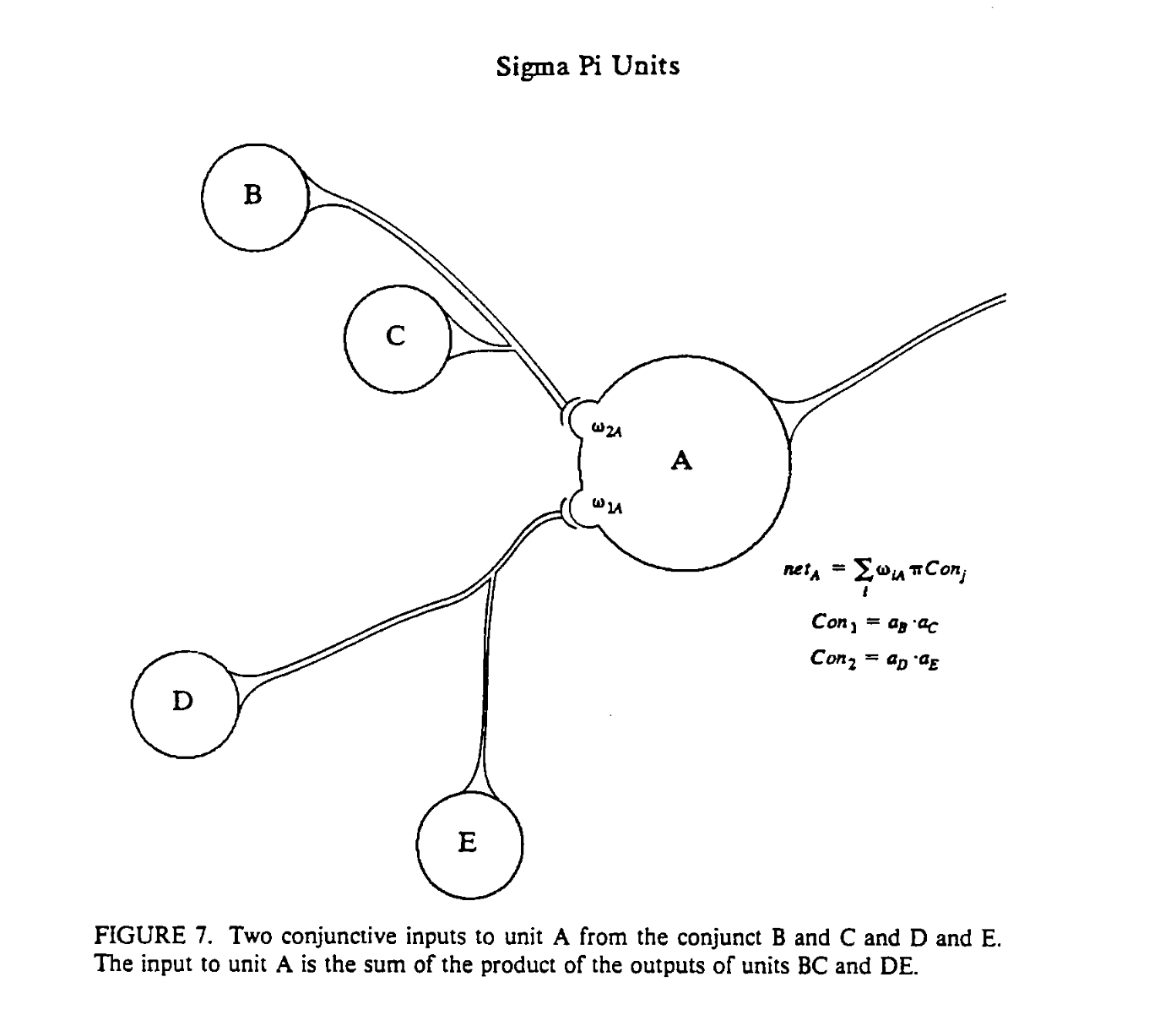
Sigma-Pi Unit

Note

This module takes his name for its sum (\sum - sigma) and muliplication (\prod - pi) operations

Thise module multiply the input for the output of another network:


\begin{aligned}
    W &= \vec{z} \times U &
        \vec{z} \in \R^{1 \times b}, \,\, U \in \R^{b \times c \times d}\\
    \vec{y} &= \vec{x} \times W &
        \vec{x} \in \R^{1 \times c}, \,\, W \in \R^{c \times d}
\end{aligned}

This is equivalent to:


\begin{aligned}
    w_{i,j} &= \sum_{h = 1}^{b} z_h u_{h,i,j} \\
    y_{j} &= \sum_{i = 1}^{c} x_i w_{i,j} = \sum_{h, i}x_i z_h u_{h,i,j}
\end{aligned}

As per this paper¹ from Stanford University, sigma-pi units can be represented as this:

Assuming a_b and a_d elements of \vec{a}_1 and a_c and a_e elements of \vec{a}_2, this becomes


\hat{y}_i = \sum_{j} w_{i,j} \prod_{k \in \{1, 2\}} a_{j, k}

In other words, once you can mix outputs coming from other networks via element-wise products and then combine the result via weights like normal.

Mixture of experts

If you have different networks tranined for the same objective, you can multiply their output by a weight vector coming from another controlling network.

The controller network has the objective of giving a score to each expert based on which is the most "experienced" in that context. The more "experienced" an expert, the higher its influence over the output.


\begin{aligned}
    \vec{w} &= \text{softmax}\left(
        \vec{z}
    \right)
    \\
    \hat{y} &= \sum_{j} \text{expert\_out}_j \cdot w_j
\end{aligned}

Note

While we used a softmax, this can be replaced by a softmin or any other scoring function.

Switch Like

Note

I call them switch like because if we put z_i = 1, element of \vec{z} and all the others to 0, it results \hat{y} = \vec{x}_i

We can use another network to produce a signal to mix outputs of other networks through a matmul


\begin{aligned}
    X &= \text{concat}(\vec{x}_1, \dots, \vec{x}_n) \\
    \hat{y} &= \vec{z} \times X = \sum_{i=1}^{n} z_i \cdot \vec{x}_i
\end{aligned}

Even though it's difficult to see here, this means that each z_i is a mixing weight for each output vector \vec{x}_i

Parameter Transformation

This is when we use the output of a fixed function as weights for out network


\begin{aligned}
    W &= f(\vec{z}) \\
    \hat{y} &= g(\vec{x}W)
\end{aligned}

This is a special case of parameter transformation


f(\vec{x}) = \begin{bmatrix}
    x_1, & x_1, & \dots, & x_n, & x_n
\end{bmatrix}

or similar, replicating elements of \vec{x} across its output.

D. E. Ruhmelhart, G. E. Hinton, J. L. McClelland | A General Framework for Paralled Distributed Processing | Ch. 2 pg. 73 ↩︎

6.0 KiB Raw Permalink Blame History