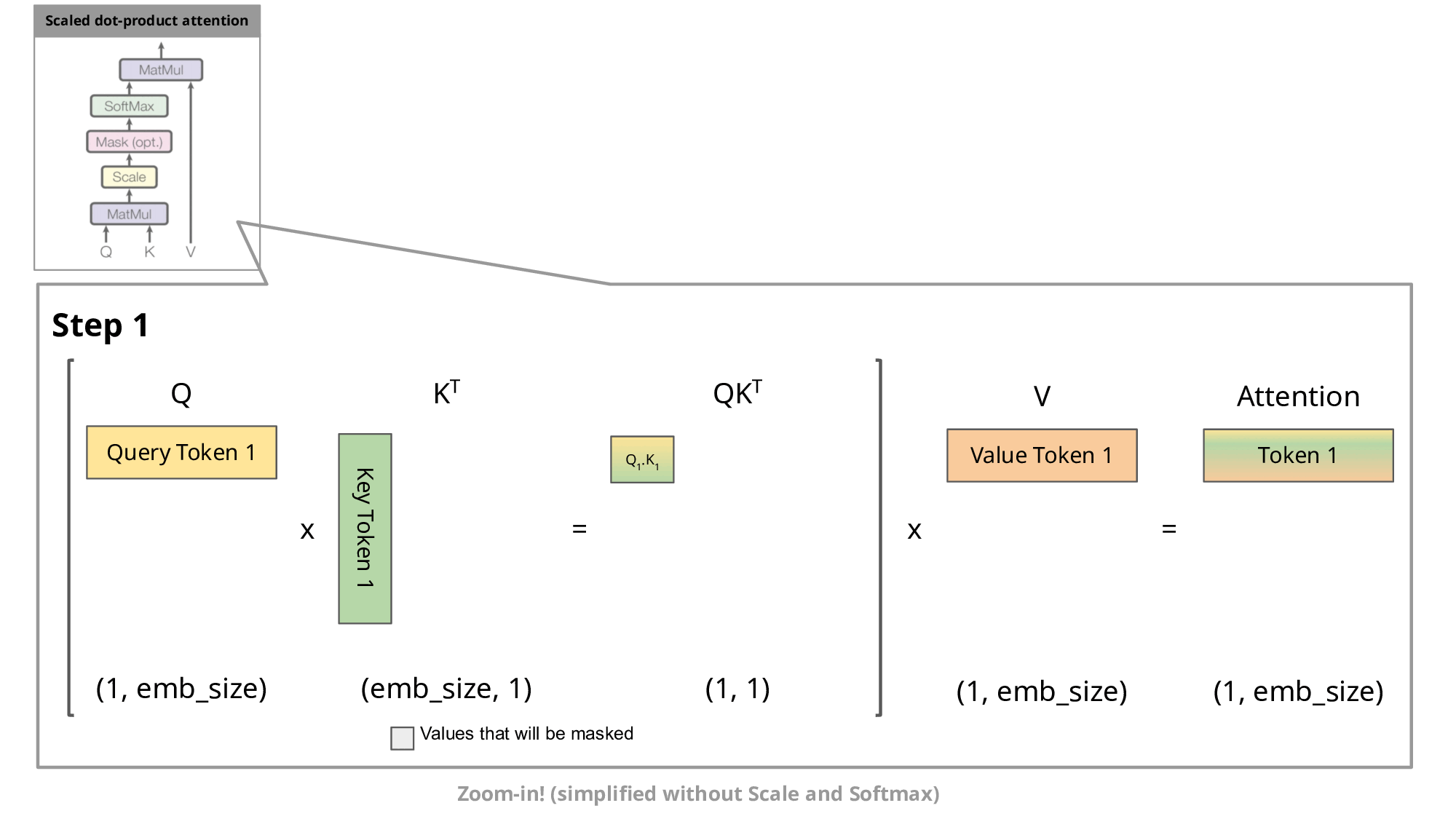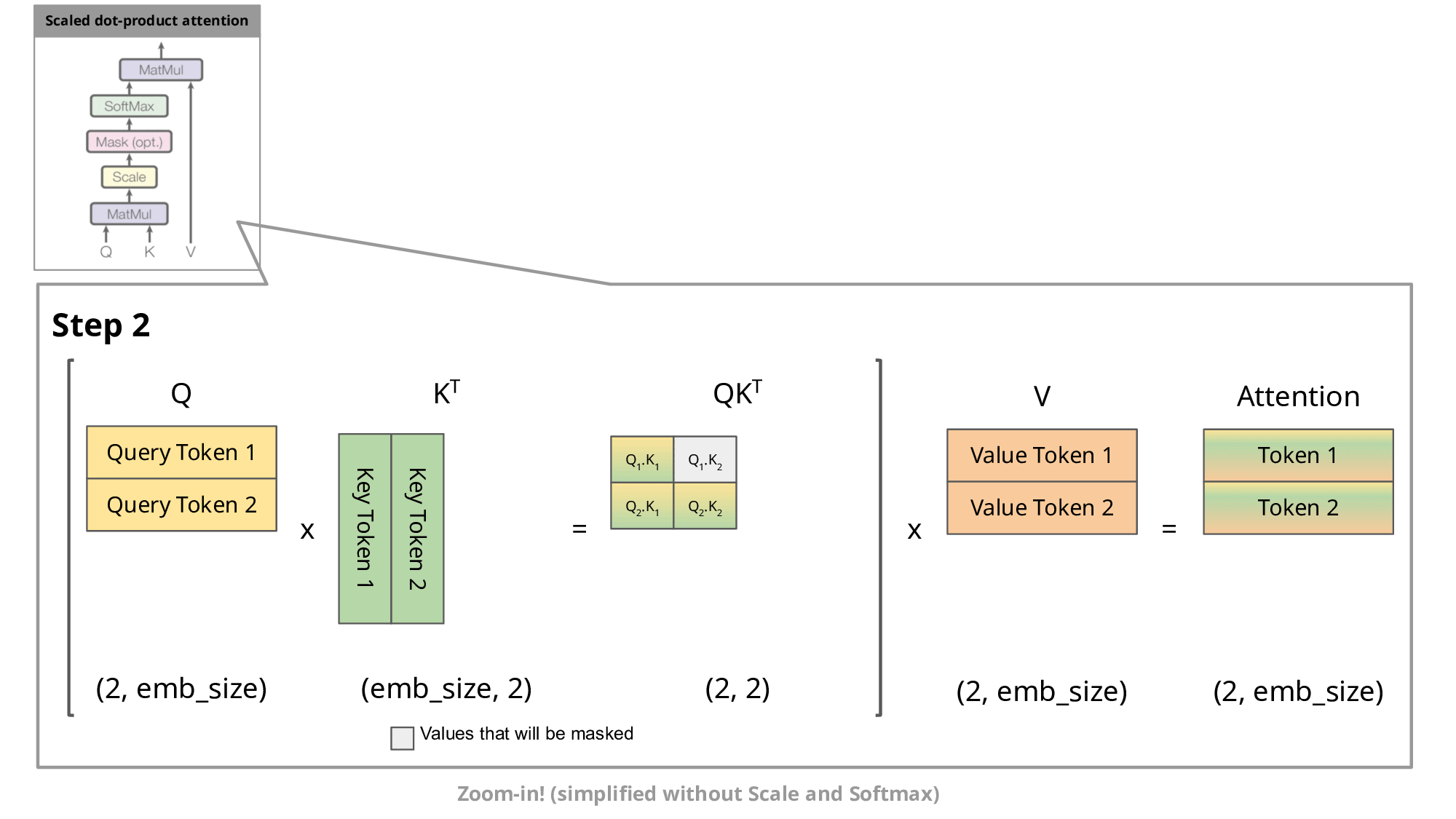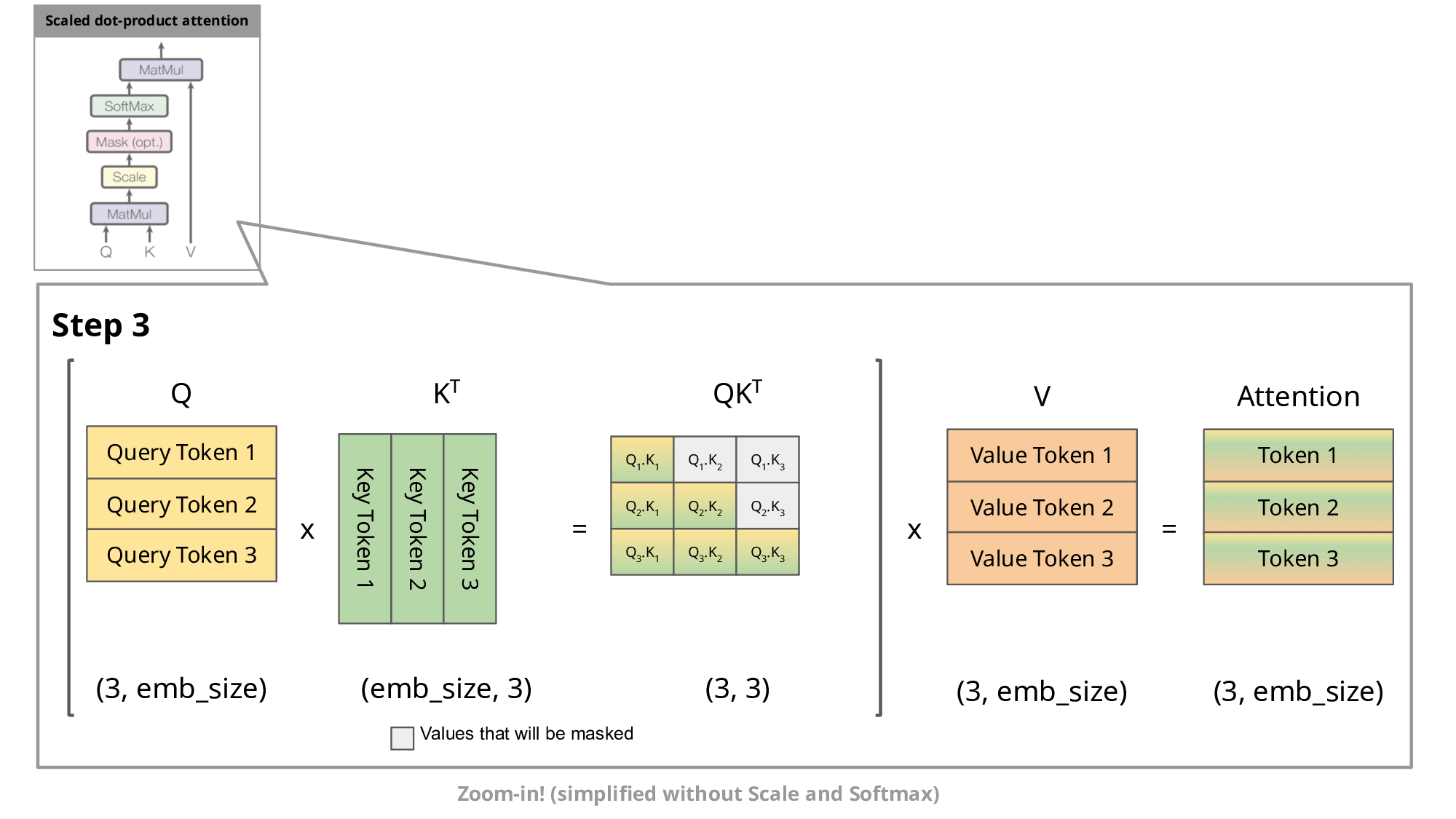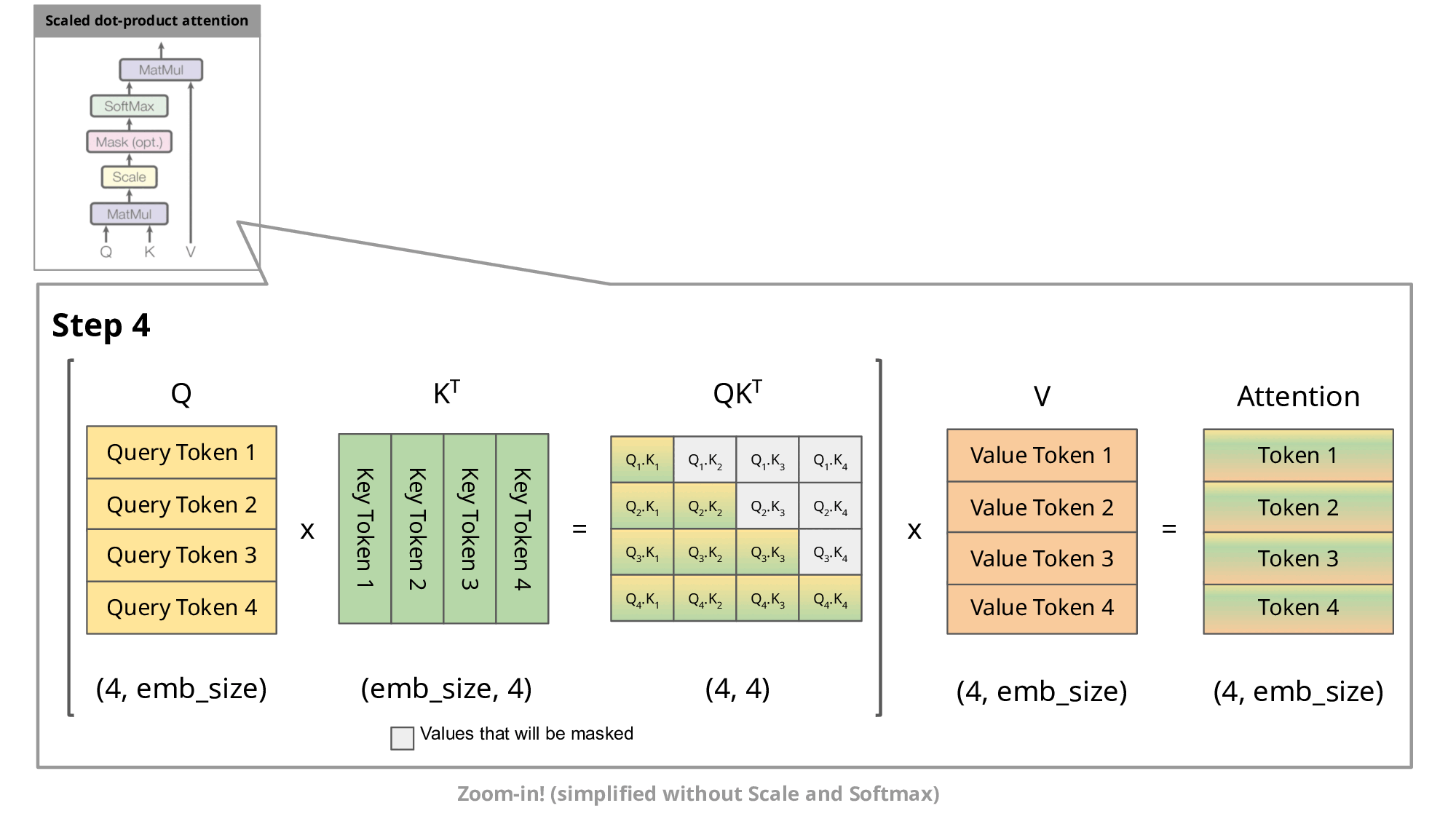
6.4 KiB
Advanced Attention
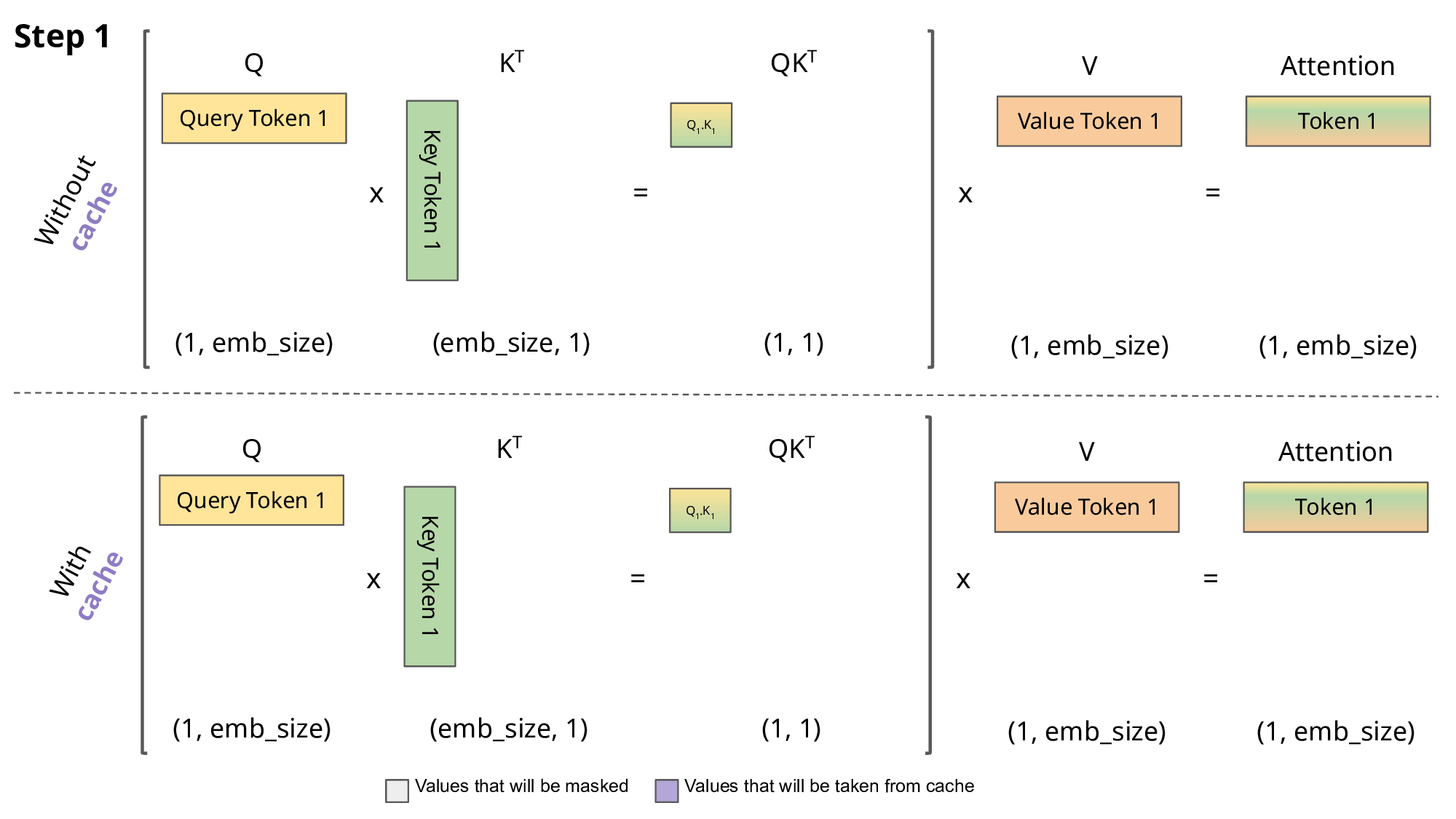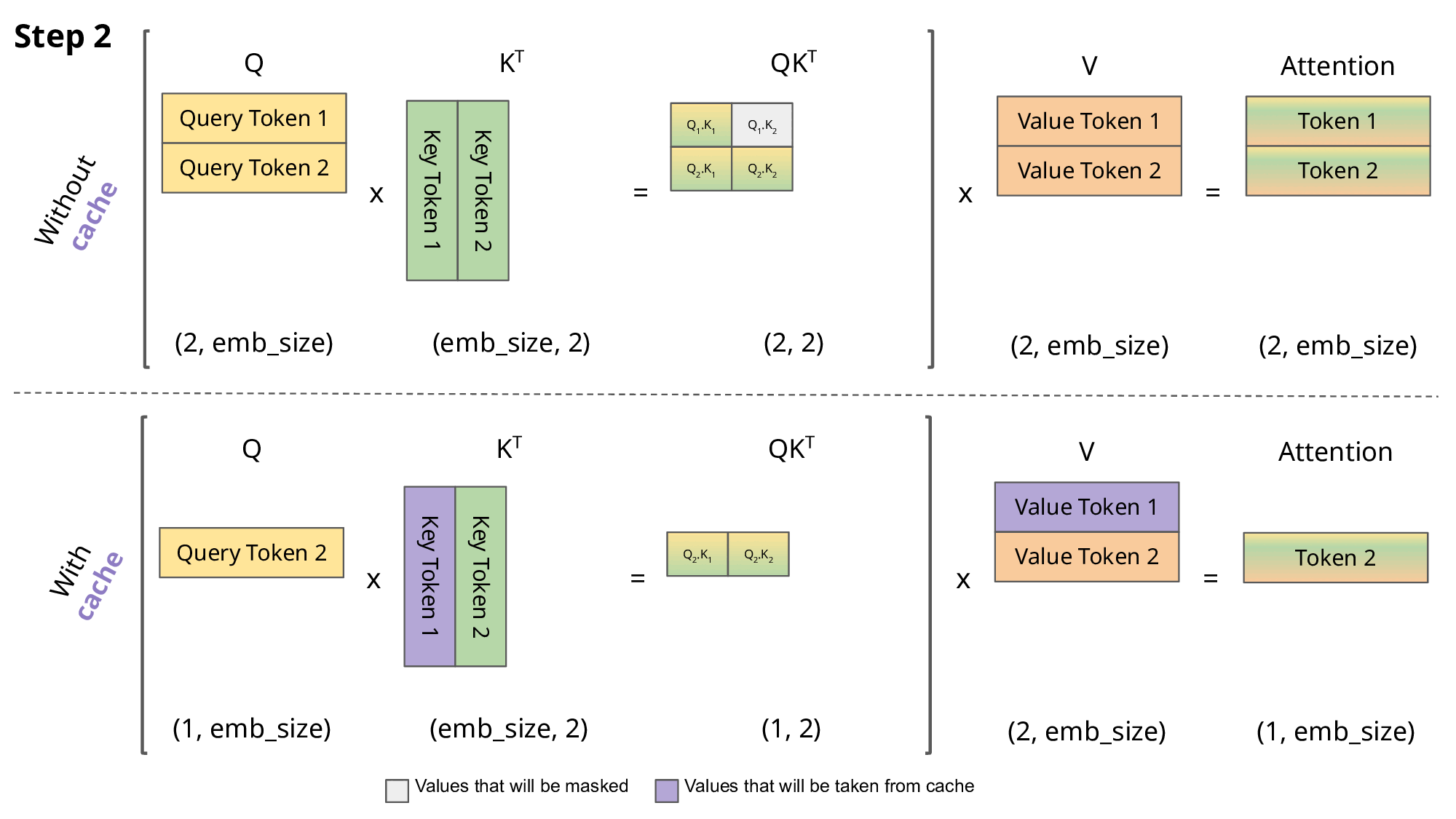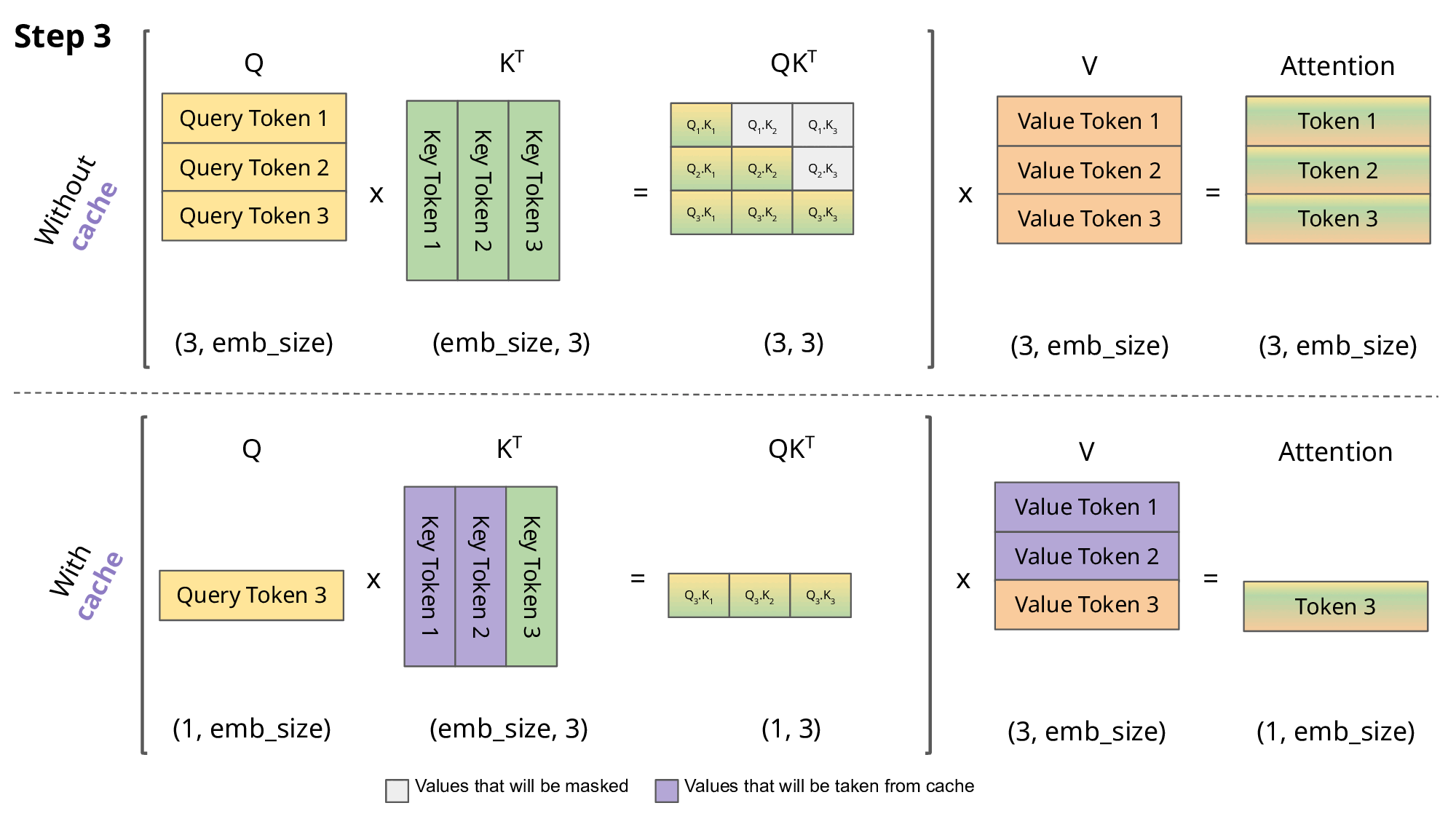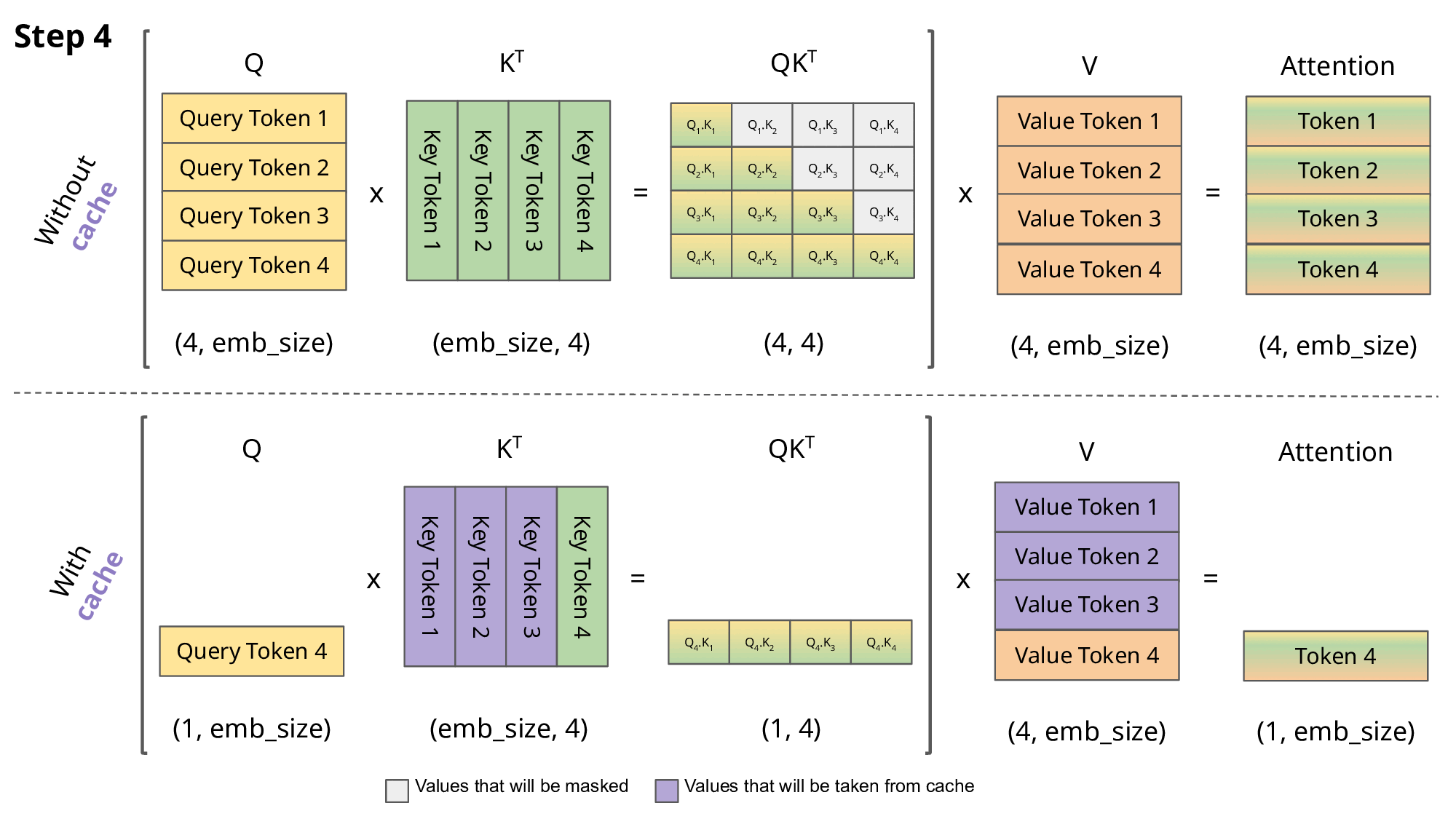
KV Caching
The idea behind this is that during autoregression in autoregressive transformers,
such as GPT, values for K and V are always recomputed, wasting computing power
GIF taken from https://medium.com/@joaolages/kv-caching-explained-276520203249
As we can notice, all tokens for previous steps gets recomputer, as well
K and V values. So, a solution is to cache all keys and values until step n
and compute only that value.
GIF taken from https://medium.com/@joaolages/kv-caching-explained-276520203249
Moreover, if we discard taking QK^T for previous steps, we can just obtain
the token we are interested in.
To compute the size needed to have a KV cache, let's go step by step:
-
For each layer, we need to store both
KandVthat are of the same dimensions (in this context), the number of heads, so the "number" ofKmatrices, the head dimension and the number of tokens incoming, the sequence lenght, and we need to know the number of bytes ford_type, usually afloat16, thus 2 Bytes:\text{Layer\_Space} = 2 \times \text{n\_heads} \times \text{d\_heads} \times \text{seq\_len} \times \text{d\_type} -
Now, during training, we pass a minibatch, so we will have a tensor of dimensions
N \times \text{seq\_length} \times \text{d\_model}. When they are processed byW_KandW_Q, we will have to store timesNmore values:\text{Batch\_Layer\_Space} = \text{Layer\_Space} \times N -
If you have
Llayers, during training, at the end you'll need space equivalent to:\text{Model\_Space} = \text{Batch\_Layer\_Space} \times L
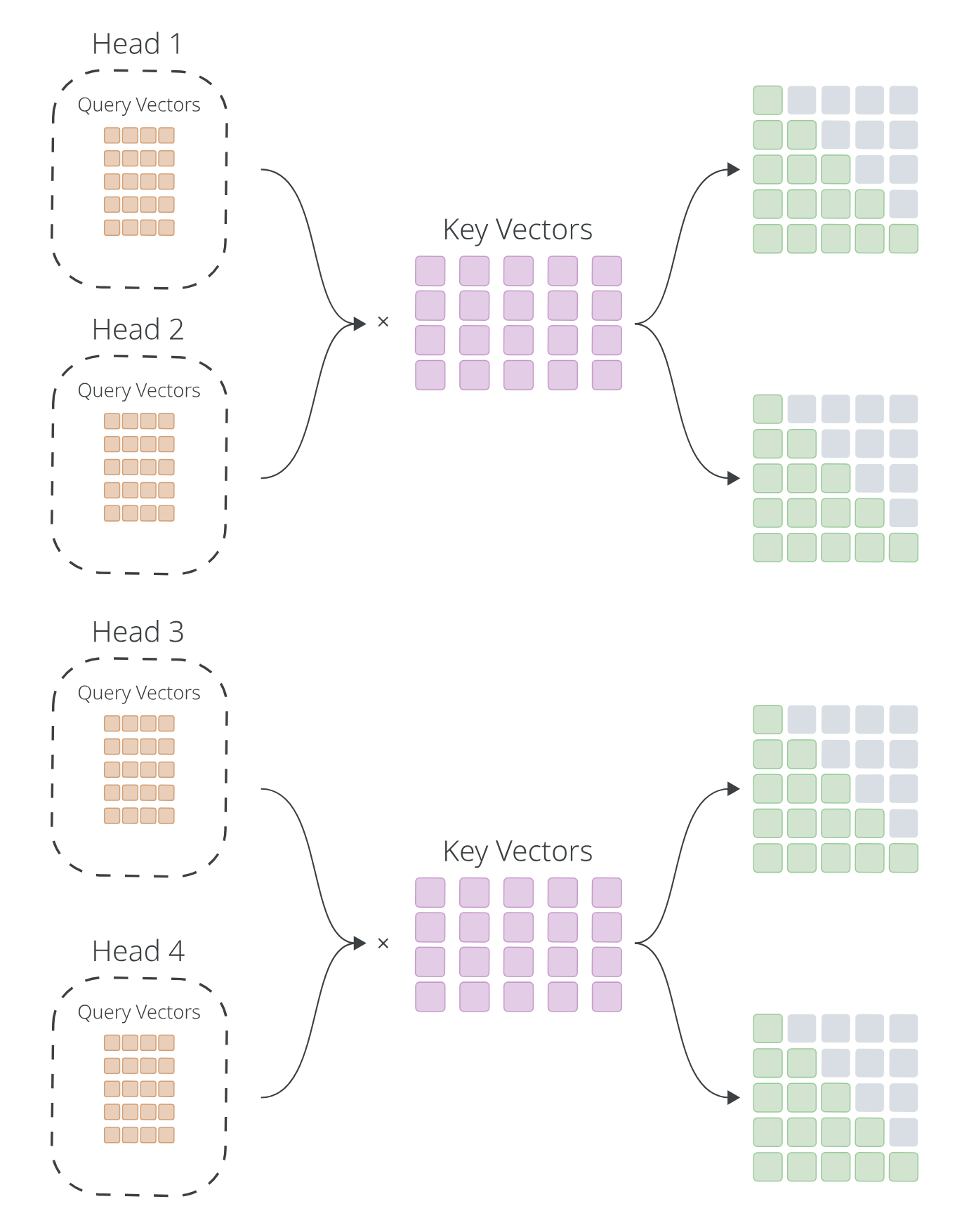
Multi-Query and Grouped-Query Attention
The idea here is that we don't need different keys and vectors, but only different queries. These approaches drastrically reduce memory consumption at a slight cost of accuracy.
In multi-query approach, we have only one K and V with a number of
queries equal to the number of heads. In the grouped-query approach, we have
a hyperparameter G that will determine how many $K$s and $V$s matrices are
in the layer, while the number of queries remains equal to the number of attention
heads. Then, queries will be grouped to some K_g and V_g
Image take from Multi-Query & Grouped-Query Attention
Now, the new layer size becomes:
\text{Layer\_Space} = 2 \times G \times \text{d\_heads} \times
\text{seq\_len} \times \text{d\_type}
Multi-Head Latent Attention
The idea is to reduce memory consumption by rank factoring Q, K, and V
computation. This means that each matrix will be factorized in 2 matrices so
that:
A = M_l \times M_r
\\
A \in \R^{in \times out}, M_l \in \R^{in \times rank},
M_r \in \R^{rank \times out}
The problem, though, is that this method introduces compression, and the lower
rank is, the more compression artifacts.
What we are going to compress are the weight matrices for Q, K and V:
\begin{aligned}
Q = X \times W_Q^L \times W_Q^R
\end{aligned} \\
X \in \R^{N\times S \times d_{\text{model}}},
W_Q \in \R^{d_{\text{model}} \times (n_\text{head} \cdot d_\text{head})}
\\
W_Q^L\in \R^{d_{\text{model}} \times rank},
W_Q^R\in \R^{rank \times (n_\text{head} \cdot d_\text{head})}
\\
\text{}
\\
W_Q \simeq W_Q^L \times W_Q^R
For simplicity, we didn't write equations for K and V that are basically
the same. However, now we may think that we have just increased the number of
operations from 1 matmul to 2 per each matrix. But the real power lies
when we take a look at the actual computation:
\begin{aligned}
H_i &= \text{softmax}\left(
\frac{
XW_Q^LW_{Q,i}^R \times (XW_{KV}^LW_{K,i}^R)^T
}{
\sqrt{\text{d\_model}}
}
\right) \times X W_{KV}^L W_{V,i}^R \\
&= \text{softmax}\left(
\frac{
XW_Q^LW_{Q,i}^R \times W_{K,i}^{R^T} W_{KV}^{L^T} X^T
}{
\sqrt{\text{d\_model}}
}
\right) \times X W_{KV}^L W_{V,i}^R \\
&= \text{softmax}\left(
\frac{
C_{Q} \times W_{Q,i}^R W_{K,i}^{R^T} \times C_{KV}^T
}{
\sqrt{\text{d\_model}}
}
\right) \times C_{KV} W_{V,i}^R \\
\end{aligned}
As it can be seen, C_Q and C_{KV} do not depend on the head, so they can be
computed once and shared across all heads, then we have
W_{Q,i}^R \times W_{K,i}^{R^T} that while it depends on the head number, it
can be computer ahead of time as it does not depend on the input.
So, for each attention head we need just 3 matmuls plus another 2 happening
at runtime. Moreover, if we want to, we can still apply caching over C_{KV}
Decoupled RoPE for Multi-Latent Head Attention
Since RoPE is a positional embedding used during attention, this causes
problems if we use a standard Multi Latent Head Attention. In fact, it
shoudl be used on both, separately though, matrices Q and K.
Since they come from C_Q \times W_{Q, i}^R and
W_{KV, i}^{R^T} \times C_{KV}^T, this means that we can't cache
W_{Q,i}^R \times W_{K,i}^{R^T} anymore.
A solution is to cache head matrices, but not their product, and compute
new pieces that will be used in RoPE and then concatenated
to the actual query and keys:
\begin{aligned}
Q_{R,i} &= RoPE(C_Q \times W_{QR,i}^R) \\
K_{R,i} &= RoPE(X \times W_{KR,i}^L)
\end{aligned}
These matrices will then be concatenated with the reconstruciton of Q and K.
References
- KV Caching Explained: Optimizing Transformer Inference Efficiency
- Transformers KV Caching Explained
- How to calculate size of KV cache
- Multi-Query & Grouped-Query Attention
- Understanding Multi-Head Latent Attention
- https://machinelearningmastery.com/a-gentle-introduction-to-multi-head-latent-attention-mla/
- DeepSeek-V3 Explained 1: Multi-head Latent Attention