Deep-Learning/Chapters/12-Transformers/INDEX.md

Transformers

Block Components

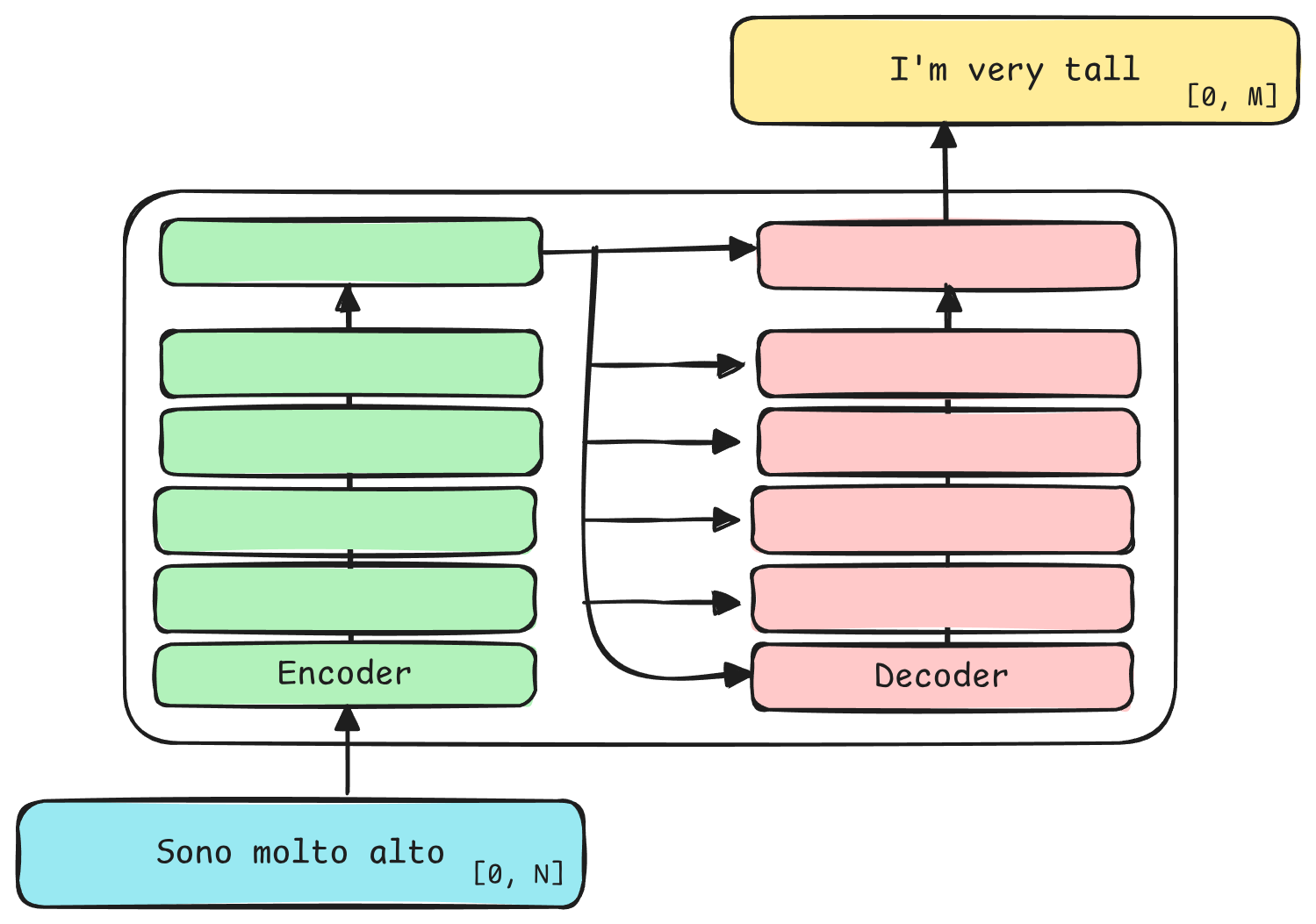
The idea is that each Transformer block is made of the same number of Encoders and Decoders

Note

Input and output are vectors of fixed size with padding

Before feeding our input, we split and embed each word into a fixed vector size. This size depends on the length of longest sentence in our training set

Embedder

While this is not a real component per se, this is the first phase before even coming to the first encoder and decoder.

Here we transform each word of the input into an embedding and add a vector to account for position. This positional encoding can either be learnt or can follow this formula:

• Even size:

\text{positional\_encoding}_{
    (position, 2\text{size})
} = \sin\left(
        \frac{
            pos
        }{
            10000^{
                \frac{
                    2\text{size}
                }{
                    \text{model\_depth}
                }
            }
        }
    \right)

• Odd size:

\text{positional\_encoding}_{
    (position, 2\text{size} + 1)
} = \cos\left(
        \frac{
            pos
        }{
            10000^{
                \frac{
                    2\text{size}
                }{
                    \text{model\_depth}
                }
            }
        }
    \right)

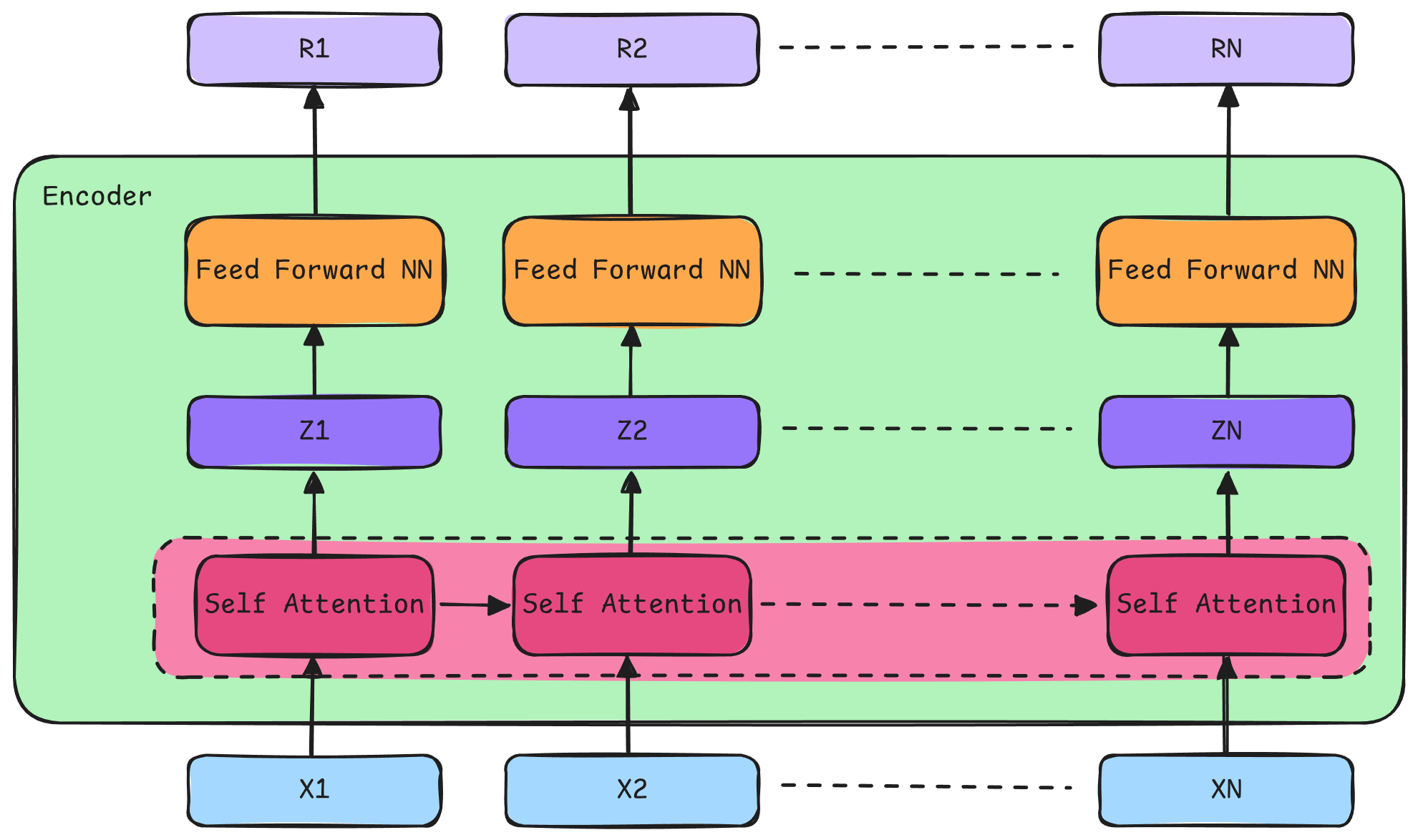
Encoder

Caution

Weights are not shared between encoders or decoders

Each phase happens for each word. In other words, if our embed size is 512, we have 512 Self Attentions and 512 Feed Forward NN per encoder

Encoder Self Attention

Warning

This step is the most expensive one as it involves many computations

Self Attention is a step in which each token gets the knowledge of previous ones.

During this step, we produce 3 vectors that are usually smaller, for example 64 instead of 512:

• Queries \rightarrow q_{i}
• Keys \rightarrow k_{i}
• Values \rightarrow v_{i}

We use these values to compute a score that will tell us how much to focus on certain parts of the sentence while encoding a token

In order to compute the final encoding we do these for each encoding word i:

• Compute score for each word j : \text{score}_{j} = q_{i} \cdot k_{j}
• Divide each score by the square root of the size of these helping vectors: \text{score}_{j} = \frac{\text{score}_{j}}{\sqrt{\text{size}}}
• Compute softmax of all scores
• Multiply softmax each score per its value: \text{score}_{j} = \text{score}_{j} \cdot v_{j}
• Sum them all: \text{encoding}_{i} = \sum_{j}^{N} \text{score}_{j}

Note

These steps will be done with matrices, not in this sequential way

Multi-Headed Attention

Instead of doing the Attention operation once, we do it more times, by having differente matrices to produce our helping vectors.

This produces N encodings for each token, or N matrices of encodings.

The trick here is to concatenate all encoding matrices and learn a new weight matrix that will combine them

Residuals

In order no to lose some information along the path, after each Feed Forward and Self-Attention we add inputs to each sublayer outputs and we do a Layer Normalization

Encoder Feed Forward NN

Tip

This step is mostly parallel as there's no dependency between neighbour vectors

Decoder

Note

The decoding phase is slower than the encoding one, as it is sequential, producing a token for each iteration. However it can be sped up by producing several tokerns at once

After the last Encoder has produced its output, K and V vectors, these are then used by all Decoders during their self attention step, meaning they are shared among all Decoders.

All Decoders steps are then repeated until we get a <eos> token which will tell the decoder to stop.

Decoder Self Attention

It's almost the same as in the encoding phase, though here, since we have no future outputs, we can only take into account only previous tokens, by setting future ones to -inf. Moreover, here the Key and Values Mappings come from the encoder pase, while the Queue Mapping is learnt here.

Final Steps

Linear Layer

Produces a vector of logits, one per each known words.

Softmax Layer

We then score these logits over a SoftMax to get probabilities. We then take the highest one, usually.

If we implement Temperature, though, we can take some tokens that are less probable, but having less predictability and have some results that feel more natural.

Training a Transformer

Known Transformers

BERT (Bidirectional Encoder Representations from Transformers)

Differently from other Transformers, it uses only Encoder blocks.

It can be used as a classifier and can be fine tuned.

The fine tuning happens by masking input and predict the masked word:

• 15% of total words in input are masked
  • 80% will become a [masked] token
  • 10% will become random words
  • 10% will remain unchanged

Bert tasks

• Classification
• Fine Tuning
• 2 sentences tasks
  • Are they paraphrases?
  • Does one sentence follow from this other one?
• Feature Extraction: "Allows us to extract feature to use in our model

GPT-2

Differently from other Transformers, it uses only Decoder blocks.

Since it has no encoders, GPT-2 takes outputs and append them to the original input. This is called autoregression. This, however, limits GPT-2 on how to learn context on input because of masking.

During evaluation, GPT-2 does not recompute V, K and Q for previous tokens, but hold on their previosu values.