Relation to Classical Control

A Brief Recap of Discrete Control

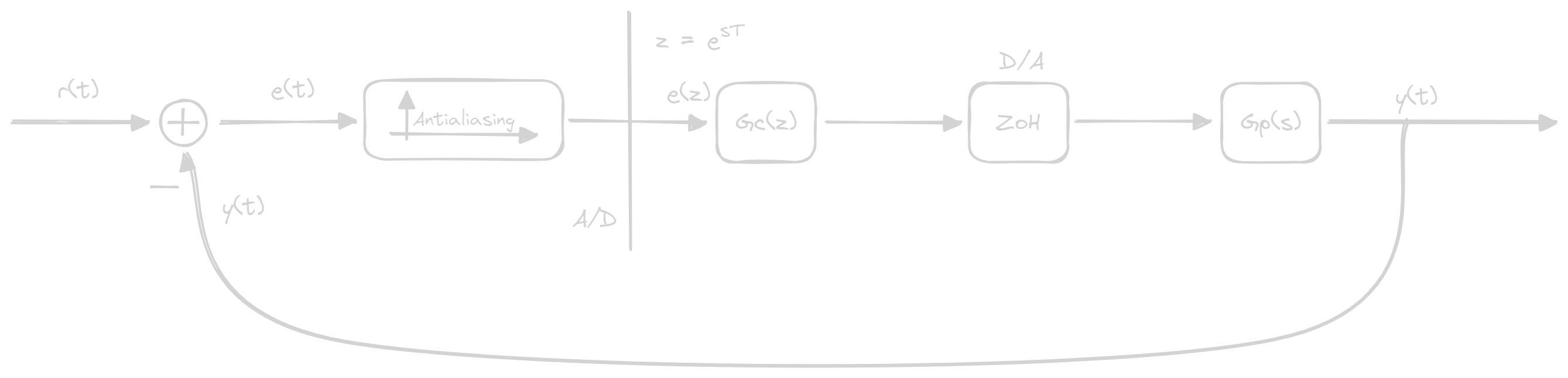
Let's say we want to control something Physical, hence intrinsically time continuous, we can model our control in the z domain and make our G_c(z). But how do we connect these systems:

Contraints

T_s: Sampling time
f_s \geq 2f_m: Sampling Frequency must be at least 2 times the max frequency of the system

Parts of the system

Take reference and output and compute the error
Pass this signal into an antialiasing filter to avoid aliases
Trasform the Laplace Transform in a Z-Transform by using the following relation:
z = e^{sT}
Control everything through a control block engineered through digital control
Transform the digital signal to an analogic signal through the use of a holder (in this case a zero order holder)
Pass the signal to our analogic plant (which is our physical system)
Take the output and pass it in retroaction

Zero Order Holder

It has the following formula:


ZoH = \frac{1}{s} \left( 1 - e^{sT}\right)

Commands:

c2d(sysc, Ts [, method | opts] )¹: Converts LTI systems into Discrete ones

Relation between `S(A, B, C, D)` to `G(s)`

From `S(A, B, C, D)` to `G(s)`

Be this our S(A, B, C, D) system:


\begin{cases}
\dot{x}(t) = Ax(t) + Bu(t) \;\;\;\; \text{Dynamic of the system}\\
      y(t) = C{x}(t) + Du(t) \;\;\;\; \text{Static of the outputs}
\end{cases}

now let's make from this a Laplace Transform:


\begin{align*}
& \begin{cases}
    sX(s) - x(0)= AX(s) + BU(s) \\
    Y(s) = CX(s) + DU(s)
  \end{cases} \longrightarrow && \text{Normal Laplace Transformation}\\


& \longrightarrow
\begin{cases}
    sX(s) = AX(s) + BU(s) \\
    Y(s) = CX(s) + DU(s)
  \end{cases} \longrightarrow && \text{Usually $x(0)$ is 0}\\


& \longrightarrow
\begin{cases}
    X(s) \left(sI -A \right) =BU(s) \\
    Y(s) = CX(s) + DU(s)
  \end{cases} \longrightarrow && \text{$sI$ is technically equal to $s$}\\


& \longrightarrow
\begin{cases}
    X(s) = \left(sI - A\right)^{-1}BU(s) \\
    Y(s) = CX(s) + DU(s)
  \end{cases} \longrightarrow && \\


& \longrightarrow
\begin{cases}
    X(s) = \left(sI - A\right)^{-1}BU(s) \\
    Y(s) = C\left(sI - A\right)^{-1}BU(s) + DU(s)
  \end{cases} \longrightarrow && \text{Substitute for $X(s)$}\\


& \longrightarrow
\begin{cases}
    X(s) = \left(sI - A\right)^{-1}BU(s) \\
    Y(s) = \left(C\left(sI - A\right)^{-1}B + D\right)U(s)
  \end{cases} \longrightarrow && \text{Group for $U(s)$}\\


& \longrightarrow
\begin{cases}
    X(s) = \left(sI - A\right)^{-1}BU(s) \\
    \frac{Y(s)}{U(s)} = \left(C\left(sI - A\right)^{-1}B + D\right)
  \end{cases} \longrightarrow && \text{Get $G(s)$ from definition}\\

\longrightarrow \;& G(s) = \left(C\left(sI - A\right)^{-1}B + D\right) && 
\text{Formal definition of $G(s)$}\\


\end{align*}

Properties

Since G(s) can be technically a matrix, this may represent a MIMO System
The system is always proper (so it's denominator is of an order higher of the numerator)
If D is 0, then the system is strictly proper and realizable
While each S(A_i, B_i, C_i, D_i) can be transformed into a single G(s), this isn't true viceversa.
Any particular S(A_a, B_a, C_a, D_a) is called realization
det(sI - A) := Characteristic Polinome
det(sI - A) = 0 := Characteristic Equation
eig(A) := Solutions of the Characteristic Equation and poles of the system
If the system is SISO and this means that C \in \R^{1,x}, B \in \R^{x,1} and D \in \R, meaning that:


\begin{align*}
  G(s) &= \left(C\left(sI - A\right)^{-1}B + D\right) =\\ 
  &= \left(C \frac{Adj\left(sI - A\right)}{det\left(sI - A\right)}B + D\right) 
  = && \text{Decompose the inverse in its formula}\\
  &= \frac{n(s)}{det\left(sI - A\right)} \in \R
\end{align*}

Note

As you can see here, by decomposing the inverse matrix in its formula it's easy to see that the divisor is a scalar, a number.

Moreover, because of how B and C are composed, the result of this Matrix multiplication is a scalar too, hence we can write this as a single formula.

Another thing to notice, regardless if this is a MIMO or SISO system is that at the divisor we have all eigenvalues of A as poles by definition

Transforming a State-Space into Another one

We basically need to use some non singular Permutation Matrices:


\begin{align*}
&A_1, B_1, C_1, D_1 \\
&A_2 = PAP^{-1} \\
&B_2 = PB \\
&C_2 = CP^{-1} \\
&D_2 = D_1
\end{align*}

Matlab Official Docs | c2d | 05 January 2025 ↩︎

4.9 KiB Raw Permalink Blame History