Deep-Learning/Chapters/5-Optimization/INDEX.md

Optimization

Beyond Full Batches

Even though full batches give the best picture of a probability dristribution of data points, it's computationally expensive.

Since data is usually highly redundant, we can think of getting smaller sets that are classes balanced, mini-batches, to update weights. While this doesn't give the same results as full batches, is still reliable.

When we need to bring things to the extreme, we can even update over a single data point, online learning, however they are not as efficient as mini-batches as they do not use matrix multiplications, which are GPU efficient

Learning rate Scheduling

Xavier-Glorot Weight initialization

Warning

Before Xavier-Glorot there was another initialization technique proportional to fan-in:

W \propto \frac{rand(in, out)}{\sqrt{in}}

Though, Xavier-Glorot is not the only available initialization as there are many others¹

Whenever we initialize weights, we need to be careful to break simmetry, as identical hiddden nodes gets the exact same results, making us lose representation power.

Another problem with weight initialization is the overshooting. This is caused by many small changes over weights. The idea to solve this is by initializing weights proprotionally to fan-in (input) and fan-out (output)

A technique we use to initialize weights comes from Xavier and Glorot, called Xavier-Glorot initialization:

\begin{aligned}
    &W \propto \frac{rand(in, out)}{in + out} \\
    &rand = \mathcal{U}(-a, a) \rightarrow a = g \cdot \sqrt{\frac{6}{in + out}} \\
    &\,\,\,\,\text{or} \\
    &rand =\mathcal{N}(0, \sigma^2) \rightarrow \sigma = g \cdot
        \sqrt{\frac{2}{in + out}}
\end{aligned}

In other words, xavier glorot extracts weights from either a uniform distribution, or a normal one, scaled by a factor g called gain

Momentum

Tip

For \beta going from 0.9 to 0.99, the learning rate needs to be decreased by a factor of 10

It's a technique inspired by physics. Imagine a ball rolling over a plane. Once it has enough speed, even if the plane changes inclination, the ball has still energy to move along the previous way because of its momentum.

Whenever on a gradient descent we have oscillations, momentum dampens all movements steering us from the previous direction. Here momentum at time k is p_k

\begin{aligned}
    p_{k+1} &= \beta p_{k} + \eta \nabla L(X, Y, W_{k}) \\
    W_{k+1} &= W_{k} - \gamma p_{k+1} \\
    \beta &\in [0, 1]
\end{aligned}

Or, in a more compact way, logically equivalent to the previous one:

    W_{k+1} = W_{k} - \gamma \nabla L(X, Y, W_{k}) + \beta(W_{k} - W_{k-1})

The larger \beta the slower it curves, accumulating more of previous directions. To play it safe, use smaller values once you are at the beginning where updates are large and slowly turn it up to values near 1

Note

• \eta: hyperparameter related to the gradient, usually equal to the learnign rate
• \gamma: Learning rate
• \beta: hyperparameter of dampening factor
• \nabla L(X, Y, W_{k}): gradient of the loss

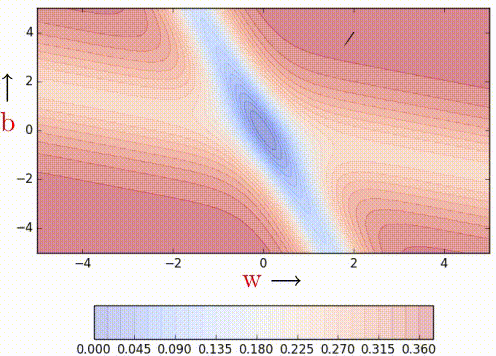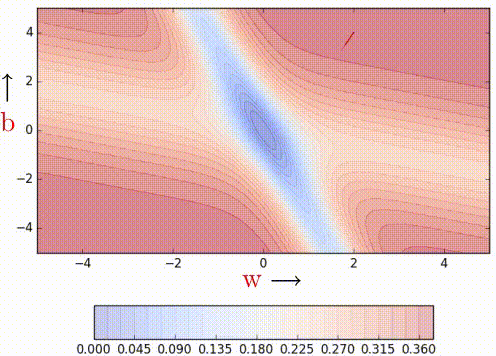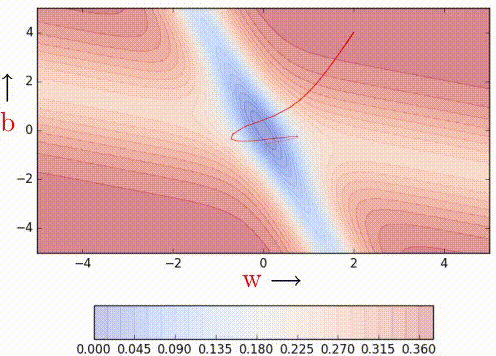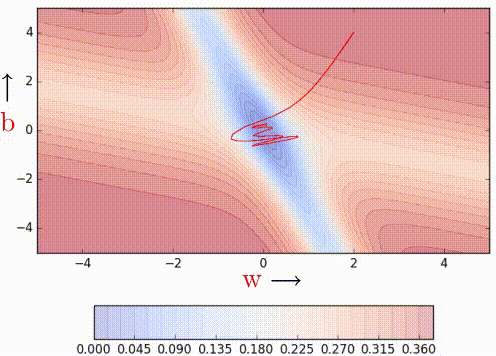
Nesterov Acceleated Gradient (aka NAG)

This method takes inpiration from Nesterov's optimization for convex functions and applies it to momentum. Its quirk is that it never computes the gradient where it lands on, but on a temporary computation of them before the actual update.

Vanilla Momentum2	Nesterov Momentum2

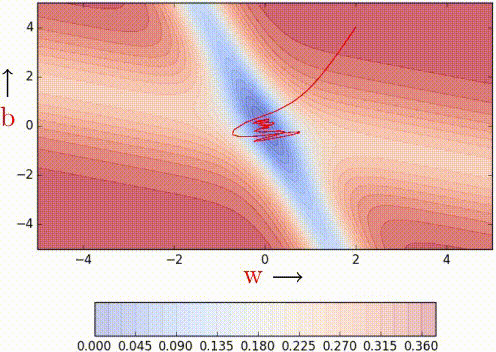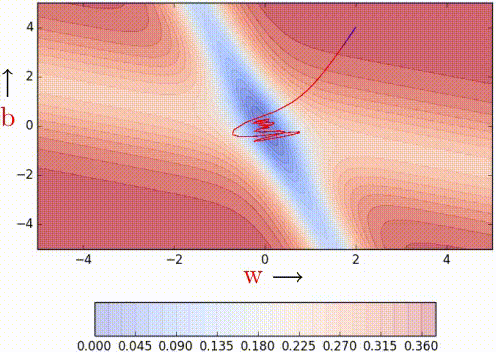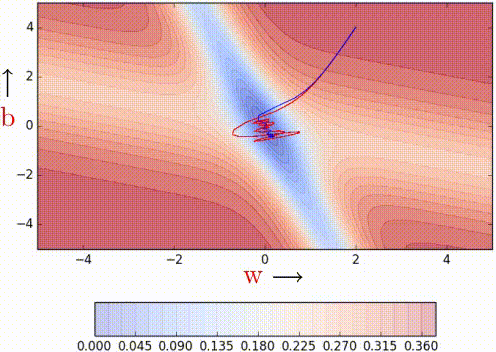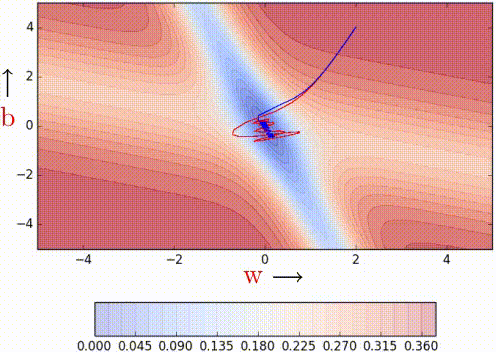To illustrate better its quirk, here's the formulation:

\begin{aligned}
    \hat{W}_{k} &= W_{k} - \beta p_k \\
    p_{k+1} &= \beta p_{k} + \eta\nabla L(X, Y, \hat{W}_k) \\
    W_{k+1} &= W_{k} - \gamma p_{k+1}
\end{aligned}

As it can be seen, the loss is computer over \hat{W}_{k} rather than W_{k} which will be our actual weights. The idea is to follow the previous momentum blindly, see where it goes and then make the correction.

Justifying Faster Optimization for Momentum Based Methods

While many people justify the speed of momentum based methods for its acceleration, this doesn't hold true as it's only accelerated for convex functions.

Since we have no idea, most of the times, how our gradient function looks like, we can't make assumptions about it being convex.

So, the most compelling explanation lies in the fact that a momentum based optimization is like computing a running average of the loss gradient, smoothing the noise introduced by the smaller sampling size. In fact, with momentum is not necessary to average steps like in SGD

Separate Adaptive Learning Rate

The idea is that each weight of each layer may need its own learnig rate to avoid overshooting and smooth the magnitude of received gradients, high over last layers and low over first ones (architecture wise)

The trick is to have a global learning rate that is adjusted by a local gain that is increased each time the weight keeps the same sign and viceversa:

\Delta w_{i,j} = - \eta \cdot g_{i,j} \frac{d \,Loss}{d \, w_{i,j}} \\

g_{i,j}(n +1 ) = \begin{cases}
    g_{i,j}(n) + 0.05 & \Delta w_{i,j}(n + 1) \cdot \Delta w_{i,j}(n) > 0 \\
    g_{i,j}(n) \cdot 0.95 & \Delta w_{i,j}(n + 1) \cdot \Delta w_{i,j}(n) < 0
\end{cases}

This method ensures that if the weight oscillates, the gain will dampen it. Moreover, should it be totally random, it will hover near 1, keeping gradient updates unchanged.

Note

The way g is updated is similar to AIMD in TCP Congestion

Tip

• Clip gains to some margins - [0.1, 10] or [0.01, 100]
• Use full batch or big mini-batches - This ensures that the change in sign is not due to sampling errors
• Combine this with momentum
• Use this to deal with axis-alignment problems

Resilient Backpropagation (aka RProp)

Instead of using the magnitude of the gradient, RProp uses the sign to derive updates that is multiplied by a step value. Here's the formulation³:

w_{i,j}^{(n)} =w_{i,j}^{(n-1)} - s_{i,j}^{(n-1)} \cdot \text{sign}\left(
    \frac{d \, Loss^{(n- 1)}}{d \, w_{i,j}}
\right) \\
s_{i,j}^{(n)} = \begin{cases}
    s_{i,j}^{(n - 1)} \cdot 1.2 &
        \text{sign}\left(\frac{d \, Loss^{(n)}}{d \, w_{i,j}}\right)
        \cdot
        \text{sign}\left(\frac{d \, Loss^{(n- 1)}}{d \, w_{i,j}}\right) > 0 \\
    s_{i,j}^{(n - 1)} \cdot 0.5 &
        \text{sign}\left(\frac{d \, Loss^{(n)}}{d \, w_{i,j}}\right)
        \cdot
        \text{sign}\left(\frac{d \, Loss^{(n- 1)}}{d \, w_{i,j}}\right) < 0
\end{cases} \\
s_{i,j} \in [10^{-6}, 50]

It is noticeable that , like separate adaptive learning rates it increase or decreases the gain. However, since it uses multiplication to increase it, makes it unusable for anything but full-batches, beacause of its fast growth.

Root Mean Square Propagation (aka RMSProp)

As the name implies, it propagates the loss over, a bit like momentum. Since RProp uses only the sign of the gradient, it's almost like dividing the gradient by its magnitude, which is bad in case of mini-batches, as all divisors are different.

RMSProp solves this by keeping the gradient magnitude similar across mini-batches by keeping a running average of it:

L^{(k)} = \beta L^{(k-1)} + (1 - \beta) \left(
    \frac{d \, Loss}{d\, W^{(k -1)}}
    \right)^2 \\
W^{(k)} = W^{(k-1)} - \eta \frac{1}{\sqrt{L^{(k)}}}\frac{d \, Loss}{d\, W^{(k -1)}}\\
     \text{usually } \beta = 0.9

What this method does is keeping a running average of the measn square error, hence the name, and use it to normalize the gradient keeping it similar across mini-batches.

Note

While it can be used with momentum, it doesn't seem to add as much benefits as using it standalone.

With Nesterov, it works best if used to normalize the correction, rather than the jump. While for the adaptive learning rates, it still requires further investigations to prove the efficacy.

Adaptive Gradient Methods

AdaGrad⁴

AdaGrad is an optimization method aimed to:

"find needles in the haystack in the form of very predictive yet rarely observed features" ⁵

AdaGrad, opposed to a standard SGD that is the same for each gradient geometry, tries to incorporate geometry from earlier iterations.

AdaGrad Algorithm

Instead AdaGrad takes another approach⁶⁵:

\begin{aligned}
    g_{i}^{(k + 1)} &= \frac{d \, Loss}{d \, w_{i}^{(k)}} \\
    G^{(k + 1)} &= \sum_{\tau = 1}^{t} g^{(\tau)} g^{(\tau)T}\\
    w_{i}^{(k + 1)} &=
    w_{i}^{(k)} - \eta \cdot\frac{
        1
    }{
        \sqrt{G_{i,i}^{(k +1)} + \epsilon}
    } \cdot g_{i}^{(k+1)} \\

\end{aligned}

Here G^{(k)} is the sum of outer product of the gradient until time t, though usually it is not used G_t, which is impractical because of the high number of dimensions, so we use diag(G_t) which can be computed in linear time⁵

The \epsilon term here is used to avoid dividing by 0⁶ and has a small value, usually in the order of 10^{-8}

Note

This example is tough to understand if we where to apply it to a matrix W instead of a vector. To make it easier to understand in matricial notation:

   \begin{aligned}
        \nabla L^{(k + 1)} &= \frac{d \, Loss^{(k)}}{d \, W^{(k)}} \\
        G^{(k + 1)} &= G^{(k)} +(\nabla L^{(k+1)}) ^2 \\
        W^{(k+1)} &= W^{(k)} - \eta \frac{\nabla L^{(k + 1)}}
                {\sqrt{G^{(k+1)} + \epsilon}}
    \end{aligned}

Note

In other words, compute the gradient and scale it for the sum of its squares until that point

AdaGrad effectiveness⁷

• When we have many dimensions, many features are irrelevant
• Rarer Features are more relevant
• It adapts \eta to the right metric space by projecting gradient stochastic updates with Mahalanobis norm, a distance of a point from a probability distribution.

AdaGrad Considerations

• It eliminates the need of manually tuning the learning rates, which is usually set to 0.01
• The squared gradients are accumulated during iterations, making the learning-rate become smaller and smaller, thus becoming 0 and untrainable

AdaDelta⁸

ADADELTA was inspired by AdaGrad and created to address some problems of it, like sensitivity to initial parameters and corresponding gradient⁸

To address all these problems, ADADELTA accumulates gradients over a window as a running average, rather than accumulating it over all instances:

G^{(k+1)} = \beta \cdot G^{(k)} +
    (1 - \beta) \cdot \nabla L^{(k+1)}

The update, which is very similar to the one in AdaGrad, becomes:

\begin{aligned}
    W^{(k+1)} &= W^{(k)} - \eta \frac{\nabla L^{(k + 1)}}{\sqrt{G^{(k+1)} + \epsilon}}
\end{aligned}

Technically speaking, the last equation is basically equivalent to the RMSProp one, as G is equivalent to the running average of the mean square.

However, as the author pointed out⁹, this equation does not respect units of measures. We should correct this problem by considering the curvature locally smooth and taking an approximation of it at the next step, becoming:

\begin{aligned}
    \Delta W^{(k)} &= - \frac{\sqrt{S^{(k-1)}}}{\sqrt{G^{(k)}}}
        \nabla L^{(k)}\\
    S^{(k)} &= \beta S^{(k - 1)} + (1 - \beta) \Delta W^{2(k)} \\
    W^{(k +1 )} &= W^{(k)} + \Delta W^{(k)}
\end{aligned}

As we can notice, the learning rate completely disappears from the equation, eliminating the need to set one

Warning

Here \Delta W is already negative, that's why there's a + in the last equation

Adaptive Moment Estimation (aka AdaM)

AdaM computes both the momentum and the squared gradients with running averages, which are 0 filled at time k = 0:

\begin{aligned}
    M^{(k+1)} &= \beta_1 M^{(k)} + (1 - \beta_1) \nabla L \\
    V^{(k+1)} &= \beta_2 V^{(k)} + (1 - \beta_2) \nabla L^2 \\
\end{aligned}

Warning

The squared gradient can be thought as the variance, however it's not centered

Then it corrects them to be used in the final formulation:

\begin{aligned}
    \hat{M}^{(k+1)} &= \frac{M^{(k+1)}}{1 - \beta_1^{k + 1}}  \\
    \hat{V}^{(k+1)} &= \frac{V^{(k+1)}}{1 - \beta_2^{k + 1}} \\
\end{aligned}

Warning

\beta_1 and \beta_2 are put to the power of k + 1, the timestep.

Then it computes the update in this way:

W^{(k + 1)} = W^{(k)} - \eta \frac{\hat{M}^{(k + 1)}}
    {\sqrt{\hat{V}^{(k+1)}} + \epsilon}

Even though Adam works, it doesn't generalize well and, particularly in image problems, it perform worse than standard SGD. Moreover, we need to keep 3 buffers instead of 1 as for SGD, which 2 of them need parameters tuning.

Note

Author proposed values are \beta_1 = 0.9, \beta_2 = 0.999 and \epsilon = 10^-8

AdamW

AdamW, tries to solve AdaM problems by introducing weight decay. In all honesty, AdaM already implements it, however it is usually added to momentum, getting scaled by \sqrt{\hat{V}}:

W^{(k + 1)} = W^{(k)} - \eta \frac{\hat{M}^{(k + 1)} + \alpha W^{(k)}}
    {\sqrt{\hat{V}^{(k+1)}} + \epsilon}

AdamW authors saw that this was inefficient as it was influences by the uncentered variance, thus modified the formula to this:

W^{(k + 1)} = W^{(k)} - \eta \frac{\hat{M}^{(k + 1)} }
    {\sqrt{\hat{V}^{(k+1)}} + \epsilon} + \lambda W^{(k)}

Lion (evoLved sIgn mOmeNtum)¹⁰

Lion is the result of a genetic search algorithm aimed to find the best optimizer.

It starts from a population of AdamW algorithms to speed up the search. Opposed to Adam and AdamW, it keeps track only for the momentum and gradient sign, requiring less memory.

Since uniform updates yields larger norms, Lion requires a smaller learning-rate and a larger decoupled weight-decay $\lambda$¹¹.

The advantages of Lion over Adam and AdamW increase with the size of the mini-batch¹¹

Symbolic Representation¹²

New trained algorithms are represented simbolically, bringing these advantages:

• Algorithms must be implemented as programs
• It easier to analyze, comprehend and transfer to new task these algorithms, rather than other algorithms such as NeuralNetworks
• We can estimate the complexity by looking at the length of code

Tournament¹³

The best code is found with a tournament style evolution. Each cycle it picks the best algorithm which will be copied and mutated and the oldest is removed

Hessian Free Optimization

Since we are moving on a function which gradient is not constant, by looking at the curvature, Hessian Matrix, we can see when it starts to change.

Newton's Method

This method would technically give us the solution in one step on a quadratic function, but it is unfeasible due to the memory and computational requirements:

\Delta W = - \epsilon H(W)^{-1} \times \frac{d\, L}{d\, W}

Conjugate Gradient

The idea is to correct the weights so that we reduce the gradient to 0 across perpendicular directions. This means that, for each update, we are not messing up previous optimizations.

While it is usually used for quadratic error surfaces, there's a non linear variant (non-linear conjugate gradient) that usually works well. However it is also possible to approximate the true error function with a quadratic one, using the standard method.

It gives a solution after N steps over an N dimensional quadratic surface, however we need to penalize frequent changes in weights, especially for hidden activities of RNNs

Optimization Tricks

Input decorrelation

If you have a linear neuron, think of a Feed Forward and not of a Convolution, it's better to decorrelate input components.

A way to achieve this is through a PCA, transforming the error surface from an ellipse to a circle.

Recognize Plateaus

If we start with big learning rates, since weights gain a big magnitude, the derivative will be small and the error will not decrease significantly.

This may seem a local minima, but this is usually a plateau.

Mini-Batch Speed up

To speed up mini batch training use these methods:

• Momentum
• Separate adaptive learing rates for each parameter
• rmsprop
• Adaptive Gradients Methods

Mini-batches vs Full-Batches

The rule of thumb is to use full-batches for small datasets or small redundancy , while mini-batches for redundant datasets

---

1. Pytorch Official Docs | torch.nn.init | 18th November 2025 ↩︎

2. Akshay L Chandra | Learning Parameters, Part 2: Momentum-Based & Nesterov Accelerated Gradient Descent | 18th November 2025 ↩︎

3. Florian | RProp | 19th november 2025 ↩︎

4. Adagrad | Official PyTorch Documentation | 19th April 2025 ↩︎

5. Adaptive Subgradient Methods for Online Learning and Stochastic Optimization ↩︎

6. Vito Walter Anelli | Deep Learning Material 2024/2025 | PDF 5 pg. 43 ↩︎

7. Vito Walter Anelli | Deep Learning Material 2024/2025 | PDF 5 pg. 44 ↩︎

8. Official ADADELTA Paper | arXiv:1212.5701v1 ↩︎

9. Official ADADELTA Paper | Paragraph 3.2 Idea 2: Correct Units with Hessian Approximation | arXiv:1212.5701v1 ↩︎

10. Official Lion Paper | arXiv:2302.06675v4 ↩︎

11. Official Lion Paper| Paragraph 1 pg. 3 | arXiv:2302.06675v4 ↩︎

12. Official Lion Paper| Paragraph 1 pg. 3 | arXiv:2302.06675v4 ↩︎

13. Official Lion Paper| Paragraph 2 pg. 4-5 | arXiv:2302.06675v4 ↩︎