Control-Network-Systems/docs/Chapters/Examples/EXAMPLE-3.md

Example 3

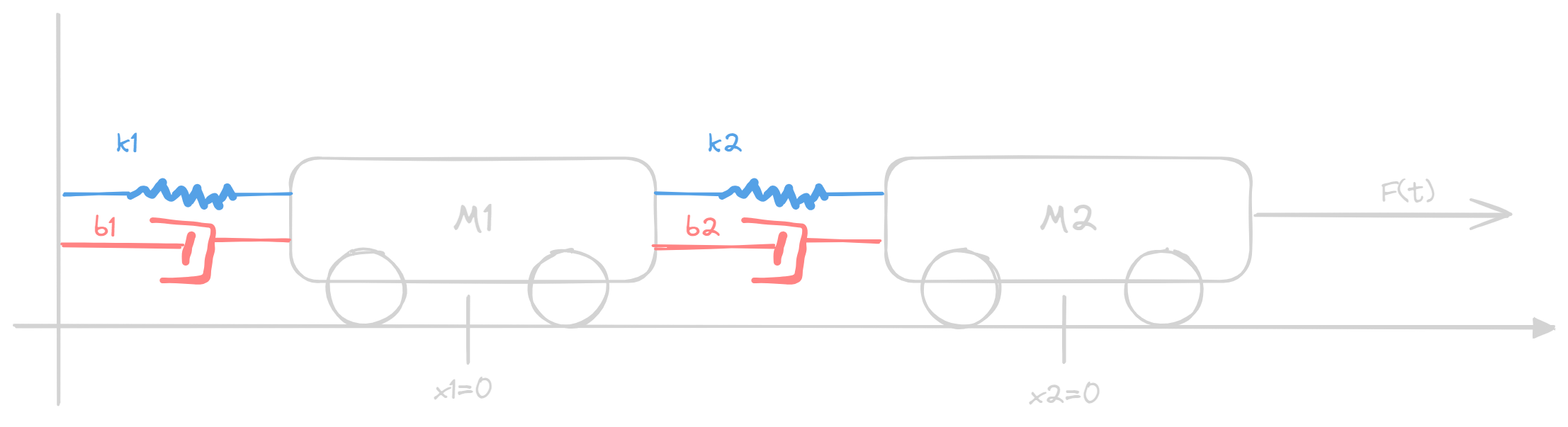
Double Mass Cart

Formulas

• Resulting forces for cart 1:
  $ m_1 \ddot{p}_1 = k_2(p_2 - p_1) + b_2( \dot{p}_2 - \dot{p}_1) - k_1 p_1 - b_1 \dot{p}_1 $

• Resulting forces for cart 2:
  $ m_2 \ddot{p}_2 = F - k_2(p_2 - p_1) - b_2( \dot{p}_2 - \dot{p}_1) $

Reasoning

We now have 2 different accelerations. The highest order of derivatives is 2 for 2 variables, hence we need 4 variables in the state:

x = \begin{bmatrix}
x_1 = p_1\\
x_2 = p_2\\
x_3 = \dot{p}_1\\
x_4 = \dot{p}_2
\end{bmatrix}

\dot{x} = \begin{bmatrix}
\dot{x}_1 = \dot{p}_1 = x_3 \\
\dot{x}_2 = \dot{p}_2 = x_4\\
\dot{x}_3 = \ddot{p}_1 = 
    \frac{1}{m_1} \left[ k_2(x_2 - x_1) + b_2( x_4 - x_3) - 
    k_1 x_1 - b_1 x_3 \right]\\
\dot{x}_4 = \ddot{p}_2 = 
    \frac{1}{m_2} \left[ F - k_2(x_2 - x_1) - b_2( x_4 - x_3) \right]\\
\end{bmatrix}

Let's write our S(A, B, C, D):

A = \begin{bmatrix}
0 & 0 & 1 & 0 \\
0 & 0 & 0 & 1 \\
% 3rd row
- \frac{k_2 - k_1}{m_1} & 
\frac{k_2}{m_1}  & 
-\frac{b_2 + b_1}{m_1} & 
\frac{b_2}{m_1} \\
% 4th row
\frac{k_2}{m_12} & 
- \frac{k_2}{m_2} & 
\frac{b_2}{m_2} & 
- \frac{b_2}{m_2} \\
\end{bmatrix}

B = \begin{bmatrix}
0 \\ 
0 \\ 0 \\ 1
\end{bmatrix}

C = \begin{bmatrix}
1 & 0 & 0 & 0 \\
0 & 1 & 0 & 0
\end{bmatrix}

D = \begin{bmatrix}
0
\end{bmatrix}

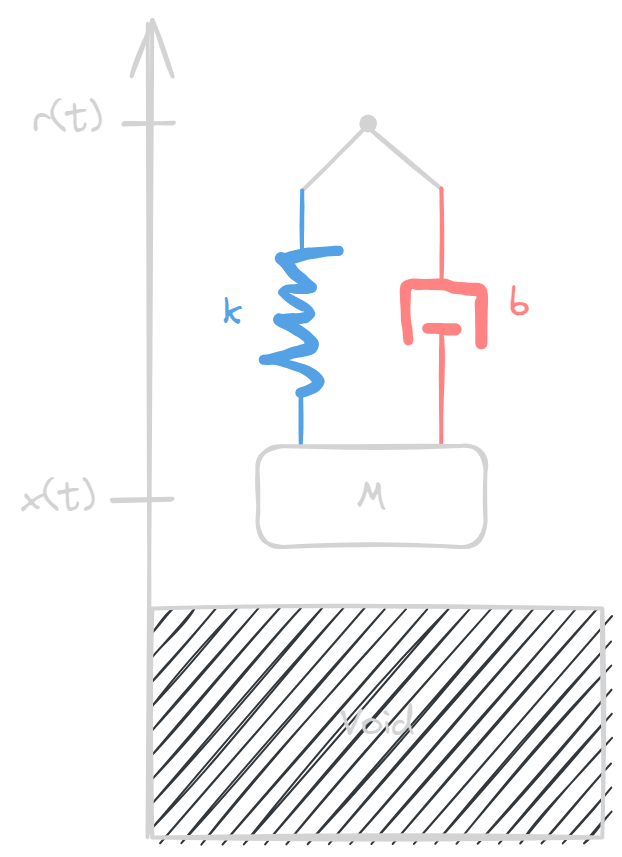
Suspended Mass

Note

For those of you the followed CNS course, refer to professor PDF for this excercise, as it has some unclear initial conditions

However, in the formulas section, I'll take straight up his own

Formulas

• Resulting forces for mass:
  $ m \ddot{p} = -k(p - r) -b(\dot{p} - \dot{r}) $

Reasoning

x = \begin{bmatrix}
x_1 = p \\
x_2 = \dot{x}_1
\end{bmatrix}

\dot{x} = \begin{bmatrix}
\dot{x}_1 = x_2 \\
\dot{x}_2 = \frac{1}{m} \left[-k(x_1 - r) -b(x_2 - \dot{r}) \right]
\end{bmatrix}

Warning

Info here are wrong

Let's write our S(A, B, C, D):

A = \begin{bmatrix}
0 & 1\\
-\frac{k}{m} & - \frac{b}{m} 
\end{bmatrix}

B = \begin{bmatrix}
0 \\ 
\frac{k + sb}{m}
\end{bmatrix}

C = \begin{bmatrix}
1 & 0 
\end{bmatrix}

D = \begin{bmatrix}
0 & 0
\end{bmatrix}